How Do You Play Third Register F Sharp On The Flute

What is a Sound Spectrum?

A audio spectrum displays the different frequencies present in a sound.

Most sounds are made up of a complicated mixture of vibrations. (There is an introduction to audio and vibrations in the certificate "How woodwind instruments work".) Perhaps yous tin hear the sound of the wind exterior, the rumble of traffic - or peradventure you take some music playing in the background, in which case at that place is a mixture of high notes and low notes, and some sounds (such as pulsate beats and cymbal crashes) which have no articulate pitch.

A sound spectrum is a representation of a sound – usually a brusque sample of a sound – in terms of the corporeality of vibration at each individual frequency. It is normally presented equally a graph of either power or pressure equally a part of frequency. The power or pressure is usually measured in decibels and the frequency is measured in vibrations per 2nd (or hertz, abbreviation Hz) or thousands of vibrations per second (kilohertz, abbreviation kHz). You can call up of the sound spectrum as a audio recipe: accept this amount of that frequency, add this amount of that frequency etc until you have put together the whole, complicated sound.

Today, audio spectra (the plural of spectrum is spectra) are usually measured using

a microphone which measures the audio pressure over a certain time interval,
an counterpart-digital converter which converts this to a serial of numbers (representing the microphone voltage) as a function of fourth dimension, and
a computer which performs a adding upon these numbers.

Your computer probably has the hardware to do this already (a sound menu). Many software packages for audio analysis or audio editing have the software that tin can take a short sample of a sound recording, perform the calculation to obtain a spectrum (a digital fourier transform or DFT) and display it in 'real time' (i.east. after a cursory delay). If how take these, you lot tin acquire a lot nearly spectra by singing sustained notes (or playing notes on a musical instrument) into the microphone and looking at their spectra. If you change the loudness, the size (or amplitude) of the spectral components gets bigger. If you alter the pitch, the frequency of all of the components increases. If you alter a sound without changing its loudness or its pitch then you are, by definition, changing its timbre. (Timbre has a negative definition - it is the sum of all the qualities that are unlike in ii unlike sounds which have the same pitch and the same loudness.) One of the things that determines the timbre is the relative size of the different spectral components. If you sing "ah" and "ee" at the same pitch and loudness, you will notice that at that place is a large departure betwixt the spectra.

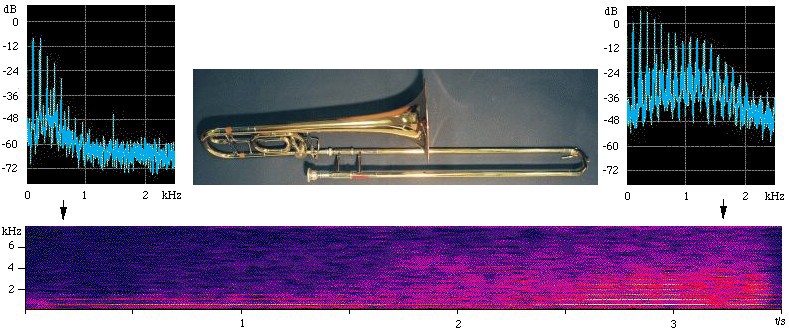
spectra and spectrogram of a crescendo

In this figure, the 2 upper figures are spectra, taken over the first and last 0.3 seconds of the sound file. The spectrogram (lower figure) shows time on the x axis, frequency on the vertical axis, and sound level (on a decibel scale) in false colour (blue is weak, red is strong). In the spectra, observe the harmonics, which appear as equally spaced components (vertical lines). In the spectrogram, the harmonics appear every bit horizontal lines. In this instance, the pitch doesn't modify, so the frequencies of the spectral lines are abiding. However the power of every harmonic increases with time, so the audio becomes louder. The higher harmonics increment more than practice the lower, which makes the timbre 'brassier' or brighter, and also makes it louder.

Spectra and harmonics

If you have tried looking at the spectrum of a musical note, or if you have looked at any of the sound spectra on our spider web pages and then you volition have noticed they accept but a small number of prominent components at a special gear up of frequencies. Here is a sound spectrum for the note G4 played on a flute (from our site on flute acoustics), which is convenient considering the pitch of this note corresponds approximately to a frequency of 400 Hz, which is round number for approximate calculations.

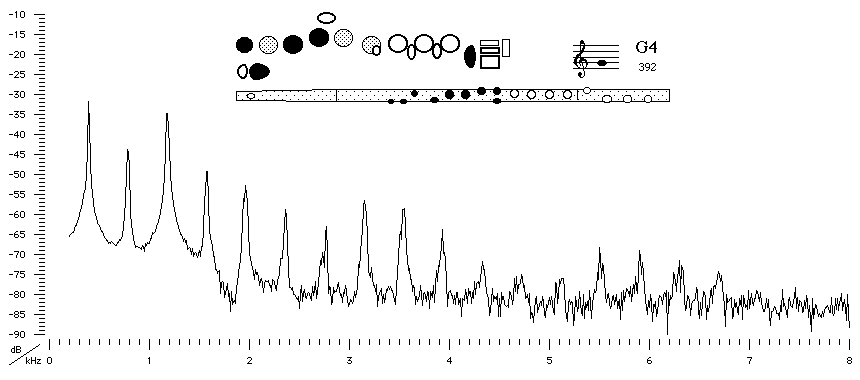
spectrum of a flute playing G4

The sound spectrum of the flute playing this annotation has a series of peaks at frequencies of

400 Hz 800 Hz 1200 Hz 1600 Hz 2000 Hz 2400 Hz etc, which we can write as:

f 2f 3f 4f ... nf ... etc,

where f = 400 Hz is the fundamental frequency of vibration of the air in the flute, and where northward is a whole number.

This series of frequencies is called the harmonic serial whose musical importance is discussed in some detail in "The Scientific discipline of Music". The individual components with frequencies nf are called the harmonics of the note.

The fundamental frequency of G4 is 400 Hz. This means that the air in the flute is vibrating with a design that repeats 400 times a second, or once every ane/400 seconds. This time interval - the time it takes before a vibration repeats - is called the period and it is given the symbol T. Here the frequency f = 400 cycles per 2nd (approximately) and the menstruation T = ane/400 second. In other words

T = 1/f.

where T is the menstruation in seconds, and f the frequency in hertz. In acoustics, it is useful to annotation that this equation works too for frequency in kHz and period in ms.

If we were to expect at the sound of a G4 tuning fork, we would find that it vibrates at (approximately) 400 times per 2nd. Its vibration is peculiarly unproblematic – it produces a smooth sine wave pattern in the air, and its spectrum has only i substantial height, at (approximately) 400 Hz. You know that the flute and the tuning fork sound different: ane way in which they are different is that they accept a different vibration pattern and a different spectrum. So let's get back to the spectrum of the flute annotation and the harmonic series. This is a harmonic spectrum, which has a special property, which we'll now examine.

Consider the harmonics of the flute note at

f 2f 3f 4f ... nf ,

The periods which stand for to these spectral components are, using the equation given in a higher place:

T T/2 T/three T/4 ... T/due north .

Consider the 2d harmonic with frequency 2f. In 1 wheel of the fundamental vibration (which takes a time T) the 2nd harmonic has exactly enough time for 2 vibrations. The third harmonic has exactly plenty time for three vibrations, and the nth harmonic has exactly enough fourth dimension for n vibrations. Thus, at the terminate of the time T, all of these vibrations are 'prepare' to start again, exactly in step. Information technology follows that any combination of vibrations which have frequencies fabricated up of the harmonic serial (i.e. with f, 2f, 3f, 4f, .... nf) will repeat exactly after a time T = 1/f. The harmonic series is special because whatsoever combination of its vibrations produces a periodic or repeated vibration at the cardinal frequency f. This is shown in the example below.

Beofre we exit this instance all the same, let'south look between the harmonics. In both of the examples shown to a higher place, the spectrum is a continuous, non-nix line, so there is acoustic power at virtually all frequencies. In the instance of the flute, this is the breathy or windy sound that is an of import part of the characteristic sound of the instrument. In these examples, this wide band component in the spectrum is much weaker than the harmonic components. We shall concentrate beneath on the harmonic components, but the wide band components are important, as well.

An example of an harmonic spectrum: the sawtooth wave

The graph below shows the starting time six harmonics of a sawtooth wave, named for its shape. On the left is the (magnitude) spectrum, the amplitudes of the dissimilar harmonics that we are going to add. The upper right figure shows six sine waves, with frequency f, 2f, 3f etc. The lower figure shows their sum. (As more than and more components are added, the figure more closely approaches the sawtooth moving ridge with its precipitous points.)